异常值对箱线图的影响分析
箱线图(Boxplot),也称为盒须图、盒式图或箱线图,是一种用作显示一组数据分散情况资料的统计图。它通过五个统计量:最小值、第一四分位数、中位数、第三四分位数与最大值来描述数据。箱线图的主要优点是对数据没有作任何限制性要求,它只是真实直观地表现数据分布的本来面貌。此外,箱线图在判断异常值时具有一定的鲁棒性,即使多达25%的数据可以变得任意远而不会很大地扰动四分位数,所以异常值不能对这个标准施加影响。
异常值的定义与识别
在统计学中,异常值(也称为离群点)是指那些显著偏离其它观测值的数值。在箱线图中,异常值通常指的是小于Q11.5IQR或大于Q3+1.5IQR的值,其中IQR为上四分位数和下四分位数的差距。这种方法的依据是,上下四分位数到边缘的长度并不一定相等,而是由满足条件的数据点决定的:上四分数到上四分位数+1.5IQR范围内,最远的数据点。
异常值对箱线图的影响
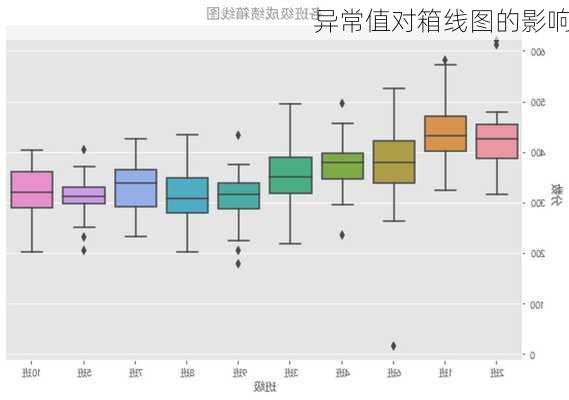
尽管箱线图在识别异常值时具有一定的鲁棒性,但实际上异常值的存在仍然会对箱线图产生影响。异常值可能导致箱线图的形状发生变化,特别是在数据分布偏斜的情况下。例如,如果数据存在大量的右偏异常值,箱线图可能会显示出较长的右须。此外,异常值还可能影响箱线图中其他统计量的计算,如中位数和四分位数。
异常值的处理
在实际的数据分析过程中,对于箱线图中识别出的异常值,通常会选择进行处理。常见的处理方法包括删除异常值、替换异常值或使用统计方法进行平滑。具体的选择取决于异常值的性质以及分析的目的。在某些情况下,如果异常值的数量较少且不影响数据分析的结果,可以选择保留这些异常值,并在解读箱线图时给予特别的关注。总结:异常值对箱线图的影响是客观存在的,它们可能导致箱线图的形状发生变化,并可能影响到统计量的计算。然而,通过合理的异常值处理方法,我们可以确保箱线图能够真实地反映数据的分布情况,并为后续的数据分析提供有价值的信息。