3σ原则的适用场景
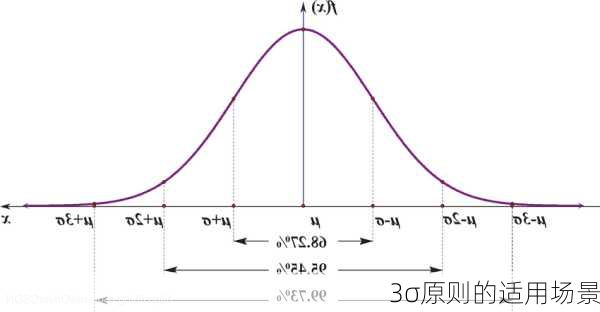
统计学中的应用3σ原则在统计学中被广泛应用,特别是在正态分布的情况下。在正态分布中,σ代表标准差,μ代表均值,x=μ即为图像的对称轴。根据3σ原则,数值分布在(μσ,μ+σ)中的概率为0.6826,数值分布在(μ2σ,μ+2σ)中的概率为0.9544,数值分布在(μ3σ,μ+3σ)中的概率为0.9974。这意味着,大部分的数据都集中在平均值的三个标准差之内,极少数的数据才会落在平均值的三个标准差之外。因此,当遇到落在(μ3σ,μ+3σ)之外的数值时,通常会被认为是异常值或离群点,并可能需要进一步的研究和处理
。
数据处理和异常值检测在数据处理和异常值检测的过程中,3σ原则是一个常用的工具。它可以帮助识别和剔除那些远离平均值的数据点,从而提高后续数据分析和建模的准确性。在机器学习中,异常检测和处理是一个重要的环节,因为异常值可能会对模型的训练和预测产生负面影响。因此,使用3σ原则对数据进行预处理,可以帮助消除这些潜在的问题
。
质量管理中的应用在质量管理中,6σ原则是一个著名的标准,它强调产品或服务的质量应该达到高度稳定和一致的状态。这里的“6σ”就是来源于3σ原则,表示在正常情况下,只有不到0.27%的产品或服务会出现质量问题。这个概念被许多大型企业采用,作为提升产品质量和服务水平的目标。通过追求6σ级别的质量标准,组织可以实现卓越的管理、强大的竞争力以及忠诚的客户
。
科学研究中的应用在科学研究中,尤其是在实验科学中,3σ原则被用来判断测量数据的可靠性和合理性。如果一组测量数据中的某个测量值的残余误差的绝对值νi>3σ,那么这个测量值就被认为可能是由于粗大误差导致的,需要被剔除。这样可以保证后续分析和结论的准确性
。
综上所述,3σ原则主要在以下几个场景中发挥作用:
1.统计学中的数据分析和建模
2.数据处理和异常值检测
3.质量管理中的追求高标准的质量目标
4.科学研究中的数据筛选和清洗