解决高维数据的降维问题
高维数据的降维问题是机器学习和数据挖掘中的一个重要环节,其目的是通过数学变换将原始高维数据转化为低维数据,以便于进一步的数据分析和挖掘。以下是解决高维数据降维问题的一些方法:
1.线性降维方法
线性降维方法主要包括主成分分析(PCA)、独立成分分析(ICA)、线性决策分析(LDA)和局部特征分析(LFA)等。
主成分分析(PCA):PCA是一种常见的数据分析方式,常用于高维数据的降维,可用于提取数据的主要特征分量。PCA的数学推导可以从最大可分型和最近重构性两方面进行,前者的优化条件为划分后方差最大,后者的优化条件为点到划分平面距离最小。
线性判别分析(LDA):LDA又称为Fisher线性判别,是一种监督学习的降维技术,也就是说它的数据集的每个样本都是有类别输出的,这点与PCA(无监督学习)不同。LDA的思想是:最大化类间均值,最小化类内方差。
2.非线性降维方法
非线性降维方法主要包括基于核函数的方法和基于特征值的方法。
基于核函数的主成分分析(KPCA):KPCA可实现数据的非线性降维,用于处理线性不可分的数据集。KPCA的大致思路是:对于输入空间中的矩阵,我们先用一个非线性映射把所有样本映射到一个高维甚至是无穷维的空间(称为特征空间),然后在这个高维空间进行PCA降维。
基于特征值的非线性降维方法:这类方法包括ISOMAP和LLE。这些方法试图在保持数据点之间相似性的前提下,将数据降到一个足够低的维度。
3.流形学习方法
流形学习方法,简称流形学习,自2000年在著名的科学杂志《Science》被首次提出以来,已成为信息科学领域的研究热点。在理论和应用上,流形学习方法都具有重要的研究意义。假设数据是均匀采样于一个高维欧氏空间中的低维流形,流形学习就是从高维采样数据中恢复低维流形结构,即找到高维空间中的低维流形,并求出相应的嵌入映射,以实现维数约简或者数据可视化。
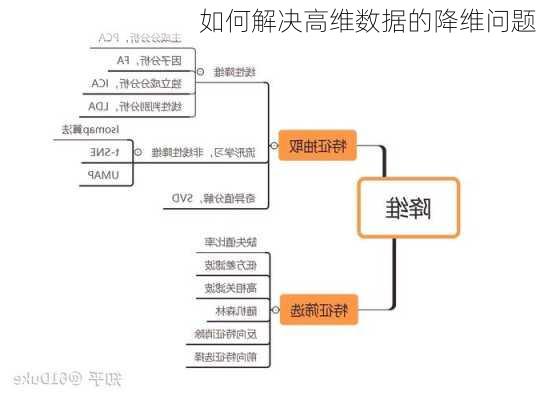
4.特征选择和特征提取
特征降维可以分为特征抽取和特征选择两种方式。特征抽取通过对原始特征空间进行变换,重新生成一个维数更小、各维之间更加独立的特征空间。特征选择则是从特征集T={t1,…,ts}中选择一个真子集T’={t1’,…,ts’},满足(s’s)。其中:s为原始特征集的大小;s’是选择后的特征集大小。
以上是一些常见的解决高维数据降维问题的方法,具体选择哪种方法取决于数据的特性和应用场景的需求。