岭回归与Lasso回归对比
岭回归和Lasso回归都是为了解决线性回归中的过拟合问题以及在通过正规方程方法求解θ的过程中出现的x转置乘以x不可逆的问题。这两种方法都通过在损失函数中引入正则化项来达到目的。
原理对比岭回归(Ridge
Regression)是一种有偏估计法,通过增加“惩罚项”来限制最小二乘法中得出的参数值,从而在回归分析中增加偏差,降低方差。这种惩罚项是对模型参数的平方和进行约束,使得回归系数不会变得比较大。Lasso回归(Least
Absolute
Selection
and
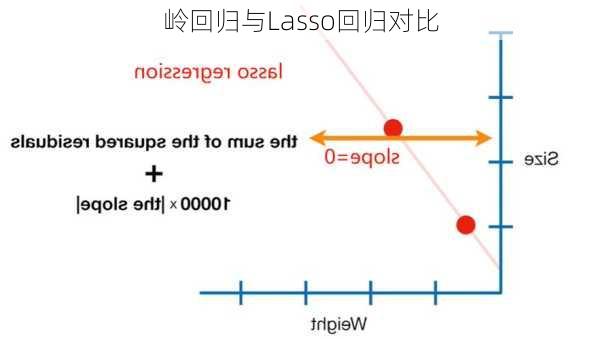
Shrinkage
Operator),则是在损失函数后,添加L1正则化。L1正则是指参数的大小限制在一个定值之内,这样可以优化特征的选择,使得无用特征的系数为0。
特点对比岭回归的特点是系数缩减,通过调节参数可以控制模型的复杂度,防止过拟合。当输入变量之间高度相关时,普通的线性回归可能会失效或产生不稳定的大系数。岭回归通过引入参数来限制系数,使得模型更加稳健。Lasso回归的特点是特征选择,由于L1惩罚项的作用,Lasso回归会将一些不重要的特征的系数压缩至零,从而实现特征选择。这使得Lasso回归产生的解是稀疏的,即大多数特征的权重会被设为零,这有助于解释和理解模型。
应用场景对比岭回归特别适用于处理多重共线性问题,当输入变量之间高度相关时,岭回归通过引入参数来限制系数,使得模型更加稳健。Lasso回归则在数据维度很高或者特征之间存在多重共线性的情况下表现出色,它可以通过调节参数来控制模型的复杂度,防止过拟合。此外,Lasso回归还能进行变量筛选,通过将某些不重要的特征的系数压缩至零,实现特征选择。
缺点对比岭回归的缺点是不进行特征选择,这可能是一个优点或缺点,具体取决于应用场景。Lasso回归的缺点是无法得出显式解,只能使用近似化的计算法估计出来的结果不太稳定,存在一定的误差。
总的来说,岭回归和Lasso回归各有优缺点,适用场景也有所不同。在实际应用中,需要根据数据的具体情况和实际需求来选择合适的方法。