数学抽象性的实例很多,下面给出几个例子:
1.自然数的抽象:自然数最初是用于表示物体个数的,比如有5个苹果,我们就用数字5来表示。但是随着数学的发展,我们开始抽象出自然数的概念,使其不仅仅局限于表示具体的物体数量,而是用来表示任意***的元素个数,甚至用于计数抽象概念的“个数”。
2.有理数的抽象:有理数可以表示为两个整数的比,例如1/2、3/4等。这种抽象使得我们可以表达那些无法用整数精确表示的比例,比如一个蛋糕被切成了若干份,我们吃掉了其中的一半,剩下的可以用有理数1/2来表示。
3.实数的抽象:实数包括有理数和无理数。有理数可以表示为有限小数或者无限循环小数,而无理数则不能。实数的引入是对数概念的一个巨大飞跃,因为它允许我们精确地表示和操作连续的量,比如长度、面积等。
4.复数的抽象:复数是由一个实数部分和一个虚数部分组成的,形式为a
+
bi,其中a和b是实数,i是虚数单位,定义为根号下1。虽然最初可能觉得没有实际意义,但复数在后来的物理、工程等领域中得到了广泛的应用,比如在交流电的分析中就扮演了重要角色。
5.向量和矩阵的抽象:向量和矩阵最初来自于物理学中的力学问题,用来表示力的大小和方向。随着时间的发展,向量和矩阵被抽象化,现在被广泛应用于物理学、计算机科学、经济学等多个领域,用来表示和解决各种问题。
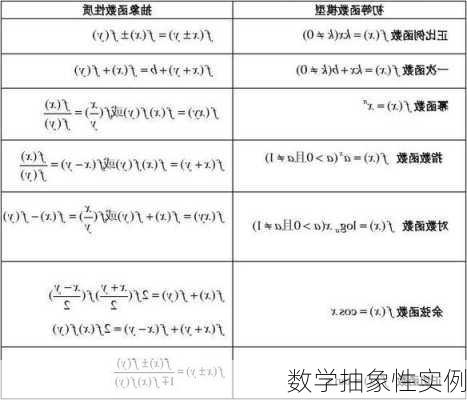
6.函数的抽象:函数最初是为了描述物理现象中变量之间的依赖关系,比如物体的位置随时间的变化。然而,随着数学的发展,函数的概念已经被高度抽象化,成为数学中的一个核心概念,用来描述任意两个***之间元素的对应关系。
这些抽象概念的形成,不仅让数学家们能够更加深入地理解和探索数学的本质,也为解决实际问题提供了强大的工具。